기초통계(2)
< 확률, 확률분포, 확률밀도함수, 확률질량함수, 독립성 검정, 적합도 검정 >
February 29, 2020
- 확률분포
- 확률밀도함수 / 확률질량함수
- 분포
- 독립성 검정
- 적합도 검정
확률
사상
- 실험이나 관측 등의 행위(시행)에 의해 생긴 결과
- ex) 주사위 던지기에서 ‘나온 눈’이 사상
확률
- 어느 사상이 어느 정도 일어나기 쉬운지(우연성의 정도)를 수치화한 것
- 모든 사상에 대한 확률을 합치면 1(100%)가 된다.
확률변수(random variable)
- 취할 수 있는 값이 확률에 의해 정의되어 있는 변수
- 시행해 봐야 비로소 결과를 알 수 있는 변수
- 이산확률변수 : 취할 수 있는 값이 1,2,3,.. 과 같이 띄엄띄엄 있어서 값의 수가 유한한 것
- 연속확률변수 : 확률변수가 취할 수 있는 값의 수가 무한한 것
확률분포(Probability distribution)
- 확률변수가 취하는 값과 그 값이 실현하는 확률의 관계
- 이산 : 균일분포, 이항분포, 포아송분포 등
- 연속 : 균일분포, 정규분포, 표준정규분포, \(X
^2\)분포, F분포, t분포
- 모든 확률변수 값이 같은 확률을 갖는 분포
- 이산균일분포 : 확률변수가 1,2,3,…이라는 이산적인 값을 취함
- ex. 주사위를 던져 각 눈이 나올 확률, 다트 게임에서 당선번호를 정할 때 각 번호가 적중할 확률
- 연속균일분포 : 값을 연속적으로 취하는 분포
- ex. 다트판의 정해진 위치부터 다트가 있었던 곳까지의 각도를 잰 값을 확률 변수라고 생각
이항분포(Binominal distribution)
- 성공이나 실패같은 사상에 대한 분포
- 결과가 두종류밖에 없는 시행(실험이나 관측 등의 행위)를 베르누이 시행이라고 함
정규분포(normal distribution)
- 좌우 대칭을 이루는 확률분포로 평균값 부근의 값일수록 관측하기 쉽다.(평균값에서 벗어날수록 관측하기 어렵다.)
- 이항분포는 시행 횟수가 많아지면 정규분포와 비슷해진다.
표준정규분포(standardized normal distribution)
- 척도가없는 분포
- 표준화 : 데아터의 평균값을 0으로, 표준편차(분산)을 1로 변환하는 것
- 변환한 데이터를 표준화변량이라고 함.
- 척도(단위)를 의식하지 않고 사용할 수 있음
- 표준화한 정규분포를 표준정규분포(z 분포)라고 한다.
- 표준화변량 Z = \(원래 데이터 - 평균 / 표준편차\)
시그마구간
- 표준화하면 데이터가 표준정규분포의 어디에 있는지 대략적인 위치를 알 수 있다.
정규분포곡선의 68-95-99.7규칙 참고!
왜도와 첨도
- 표준분포 모양이 정규분포에서 어느 정도 벗어나 있는지를 측정하기 위한 지표
- 왜도 : 분포가 좌우대칭인지, 오른쪽 꼬리가 긴지(왼쪽으로 치우쳐 있는지), 왼쪽 꼬리가 긴지(오른쪽으로 치우쳐 있는지), 분포가 좌우로 치우친 정도(비대칭도)를 나타내는 지표
- 첨도 : 분포의 산의 뾰족한 정도를 나타내는 지표
- 왜도나 첨도가 0에서 크게 벗어난 값을 취한 경우, 극단적으로 값이 크거나 작은 수치가 섞여있을 가능성이 있음
포아송 분포
- 시행횟수가 아주 많고, 사상 발생의 확률이 아주 작을 때의 이항분포
- ‘드물게 일어나는 사항’의 확률분포를 나타내는 데 이용(1회 관측에서 일어날 일이 드물지만, 일정 시간내에 어느 정도의 빈도로 일어나는 이벤트 수)
- ex)한 달에 생산한 물건 중 불량품의 수, 어느 교차점에서 교통사고가 일어나는 수, 어느 지역에 떨어지는 벼락 건수 등
개념
확률밀도함수(probability density function)
- 확률변수의 값과 확률 사이의 함수관계
- 확률밀도함수와 가로축으로 둘러싸인 면적은 1
- 확률밀도(연속확률변수가 주어진 어떤 구간 내에 포함될 확률)를 함수형태로 나타낸 것
.png)
누적분포함수(연속형)
- 연속확률변수 X가 f(x)라는 확률밀도함수를 가질 때, 실수 x에 대하여 구간(-\(\infty\),x)에서 확률값을 나타내는 함수
.png)
확률질량함수
- 이산확률변수가 가질 수 있는 모든 특성값(x)에 대한 확률을 나타내는 함수
.png)
누적분포함수(이산형)
- 이산확률변수 X가 p(x)라는 확률질량함수를 가질 때, X가 가질 수 있는 관찰값 x를 누적시켜 해당되는 확률질량함수 값을 더한 형태
.png)
척도와 변수에 따른 통계적 분석방법
데이터의 유형, 척도, 변수
- 데이터 : 수, 영상, 단어 등의 형태로 된 의미 단위로 보통 연구나 조사 등의 바탕이 되는 재료
- 질적자료 : 수치로 측정이 불가능한 자료
- 양적자료 : 수치로 측정이 가능한 자료
- 척도 : 측정하고자 하는 대상의 특성을 수량화 하기 위해 부여하는 숫자들의 체계
- 변수 : 값이 특정 지어지지 않아 임의의 값을 가질 수 있는 문자
- 독립변수(=원인변수) : 어떠한 효과를 관찰하기 위하여 실험적으로 조작되거나 혹은 통제된 변수
- 종속변수(=결과변수) : 독립변수의 효과를 측정하는 대상
각 척도별 대표값
대표값
- 주어진 자료를 대표하는 특정값으로 어떤 값들의 집합의 적절한 특징을 나타내거나 요약한 것
- 인과 관계 연구일 경우 독립변수의 숫자에 따라 표본 수 결정
모수통계, 비모수통계
- 모수통계 : 모집단의 모수에 관한 가설을 포함하는 추론적 통계
- 비모수통계 : 표본이 추출되는 모집단의 분포형태에 관한 전제를 필요로 하지 않는, 서열적인 수준의 표본자료애 관한 분석에서 사용되는 통계방법
통계분석 방법의 종류 및 개념
- 빈도분석
- T검정
- 두 표본집단간의 성격이 ‘맞다/틀리다’, ‘같다/다르다’, ‘차이가있다. 없다’의 검증
- 분산분석
- 요인분석
- 신뢰도 분석
- 연구 대상에 대해 반복적으로 측정하더라도 동일한 값을 얻을 수 있는가(신뢰도) 확인
- 연관성 분석
- 변수들 간의 관계와 연관성 강도 확인
- 변수들이 독립적(연관성 = 0)
- 변수들 간에 어떤 연관이 있는지 (0<연관성<1)
- 카이제곱분석
- 회귀분석
분포
자유도(degrees of freedom)
- 통계적 추정을 할 때 표본자료 중 모집단에 대한 정보를 주는 독립적인 자료의 수
- 표준편차 계산하는 경우의 자유도는 자료의 개수 - 1
- 표준편차 계산의 대상이 되는 편차들의 합은 0이됨. 편차들의 합이 0이 된다는 하나의 제약조건이 자유도를 1만큼 감소시킨 것임
더 자세한 설명은 여기서!
카이제곱분포(\(X^2\))
- 정규분포를 따르는 여러 데이터를 한꺼번에 취급할 수 있어, 분산분석에 이용할 수 있음
- 왼쪽으로 치우치고 오른쪽으로 긴 꼬리를 갖는 분포, 즉 양의 왜도를 갖는 분포
- 제곱하면 데이터의 수(자유도)에 따라 분포형태가 달라진다.
- 독립성 검정이나 적합도 검정에 사용
- 기대값 = 자유도 AND 분산 = 2 * 자유도
- 자유도가 늘어나면 \(X^2\) 분포의 그래프가 오른쪽으로 이동하여 평평해지는 이유
- 자유도가 커질수록 종모양의 분포 -> 정규분포에 근사
F분포(F-distribution)
- \(X^2\)값의 비
- F값은 2개의 \(X^2\)값의 비로 정의되는데, 그 분포가 F분포임.
- 각 표본의 \(X^2\)값을 사용하기 때문에 자유도가 2개 있다.
- 등분산검정과 분산분석 등에 주로 이용
t분포(t-distribution)
- 모분산을 알 수 없고 표본 크기가 작을 때, 정규분포(z분포)를 이용해 추정 또는 검정을 하면 결과가 틀릴 수 있다.
- 이럴경우 스튜던트화 변량이 따르는 t분포를 사용함.
- 표본의 크기가 작을 때는 정규본포에 비해 양쪽 꼬리가 두꺼워지지만, n>=30 근처부터는 정규분포와 거의 일치
독립성 검정, 적합도 검정
독립성 검정
- 조사대상에 대하여 두 가지 범주형 변수에 대해서 서로 관련성이 있는지 검정하는 방법
- 독립성 검정에는 크게 교차분석과 카이제곱 독립성 검정이 활용됨
적합도 검정
- 특정 분포 혹은 비율에 검정하고자 하는 대상이 얼마나 적합한가(일치하는가)에 대한 검정
- 두 모집단이 서로 동일한 분포를 가지는지 알아보기 위해 실시함
- 대표적 : 카이제곱 적합도 검정, Kolmogorov-Smirnov
오차
- 측정대상이 갖는 참값과 측정도구를 적용하여 얻은 측정값 사이의 불일치 정도(혹은 차이)
- 체계적 오차 : 변수에 일정하게 체계적으로 영향을 줌으로써 측정결과가 모두 높아지거나 낮아지게 되는 오차
- 비체계적 오차 : 오차의 값이 인위적이거나 편향된 것이 아니라, 다양하게 분산되어 있어 무작위적으로 발생하는 오차
- 표본 오차 : 표본추출 과정에서 생기는 오차(표집 오차)
- 비표본 오차 : 조사설계상의 오차와 자료처리상의 오차
신뢰도
- 측정하고자 하는 현상을 얼마나 일관성 있게 측정했는가 하는 정도(측정의 신뢰도)
- 신뢰도 측정방법 : 재검사법, 복수양식법, 반분법, 내적 일관성 분석법
- 신뢰도 제고방안
- 측정 도구의 모호성 제거
- 측정자의 태도와 측정 방식의 일관성 유지
- 측정 항목의 수를 늘림
- 조사 대상자가 잘 모르거나 무관심한 내용은 측정항목에서 제외
- 이미 신뢰도가 검증된 표준화된 측정도구를 이용
타당도
- 측정하고자 하는 개념이나 속성을 얼마나 정확히 측정했는가 하는 정도
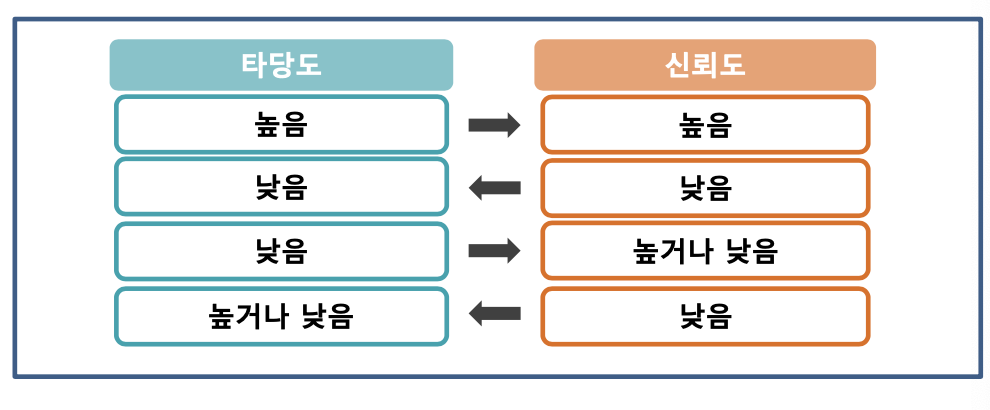
- 신뢰도와 타당도의 관계
.png)
.png)
.png)
.png)
