K-MOOC 경제통계학 1부 : 그림과 수치를 이용한 자료의 정리 강좌를 바탕으로 작성한 글입니다.

통계자료의 단위변환과 그 사례

단위 변환

• 원점수를 표준점수로 바꾸는 것
• 상수를 더하거나 곱하는 변환.
• 예: 섭씨 온도(y)=5/9(화씨 온도(x)-32). 즉 y=-160/9+(5/9)x
• 표준화(standardization): 평균을 빼주고 표준편차로 나누어 주는 변환.

• 새로운 확률변수 Z는 평균이 아니고 표준편차가 1인 분산이 1인 정규분포를 따르게 된다.
  • 1) 분포의 전반적인 모습은 단위변환에 의해서 변하지 않는다.
  • 2) 평균을 빼줬기때문에 평균은 0
  • 3) 표준편차로 나눴기때문에 새로운 편차는 1이 될 수 밖에 없다.

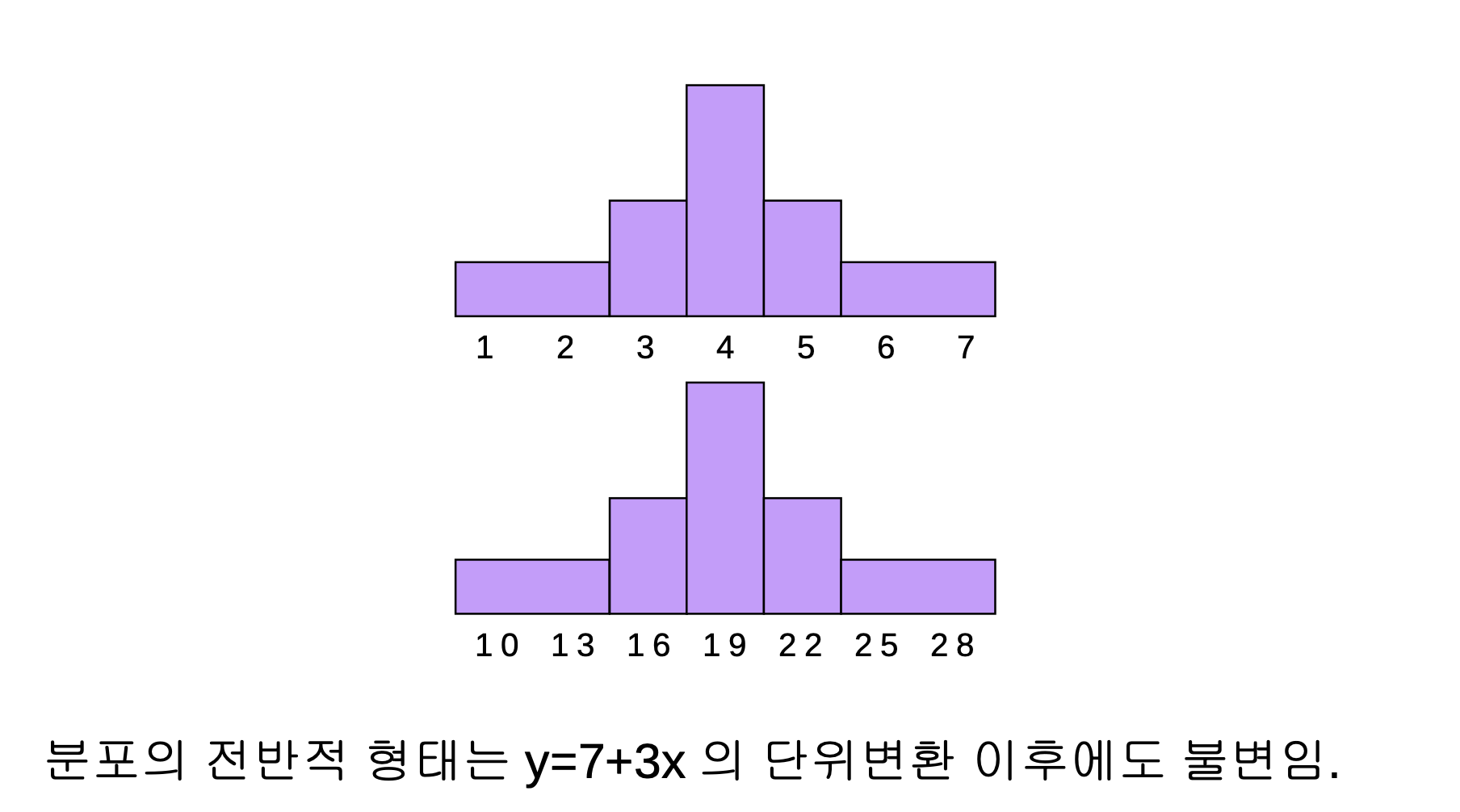
• 위치와 스케일만 달라졌을 뿐 전반적으로 달라진게 없다.

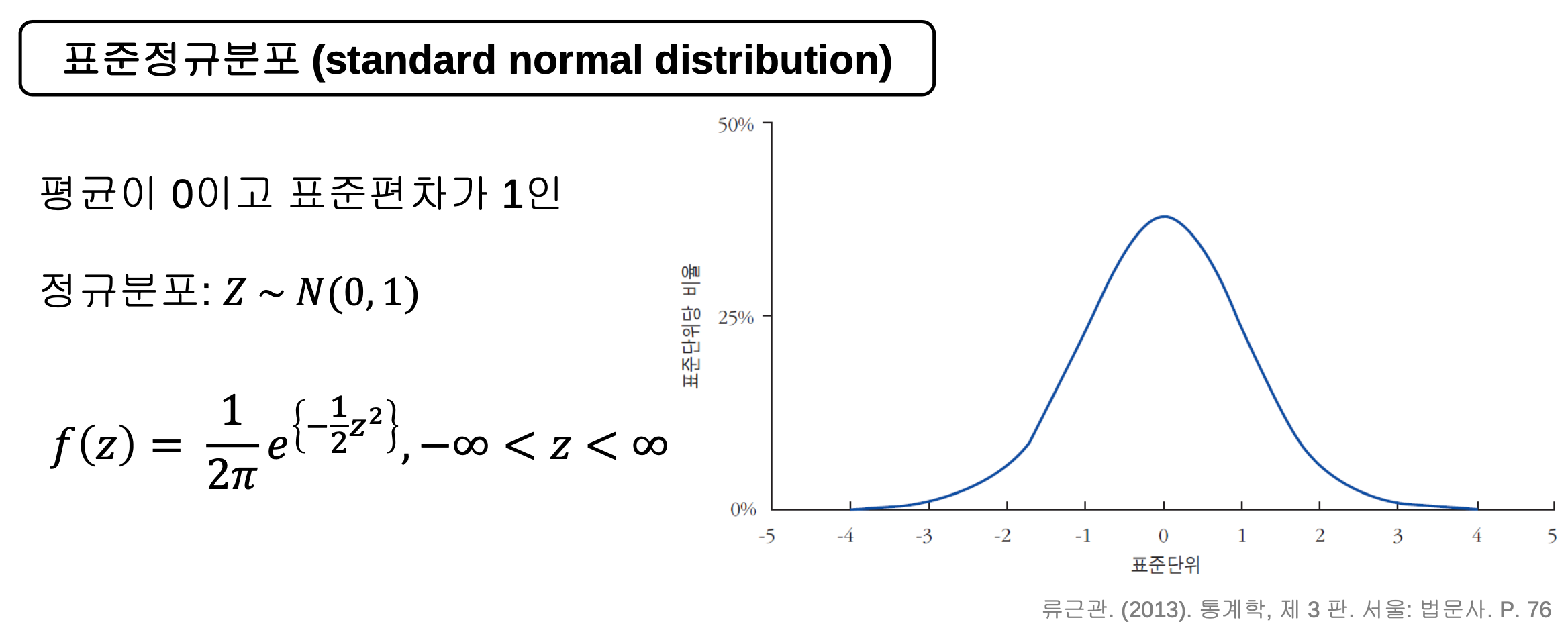
정규분포곡선의 특징

정규분포곡선

• 하나의 이상적인 히스토그램.
• 하나의 수학적 모형.
• 개념상 모집단의 분포.

• 𝜇 : 중심이 어딘지
• 𝜎 : 중심으로 부터 관측치 하나하나 즉, 확률 변수 하나를 뽑아내면 중심으로부터 표준적으로 얼마나 떨어져있을 것 같은가

정규분포곡선의 68-95-99.7 규칙

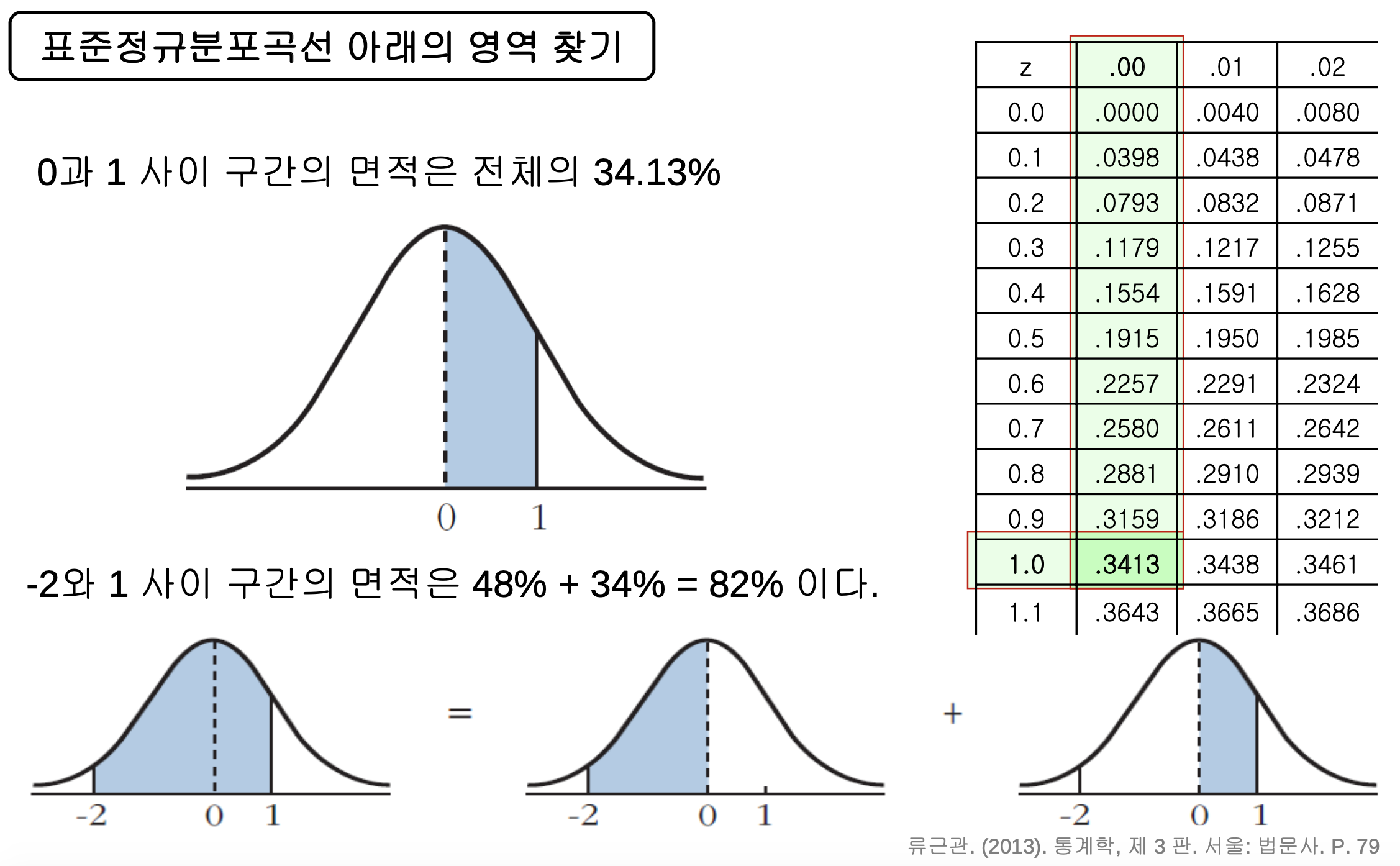
• 표준단위로 -1부터 1까지 영역의 넓이 : 전체 면적의 약68%
• 표준단위로 -2부터 2까지 영역의 넓이 : 전체 면적의 약95%
• 표준단위로 -3부터 3까지 영역의 넓이 : 전체 면적의 약 99.7%

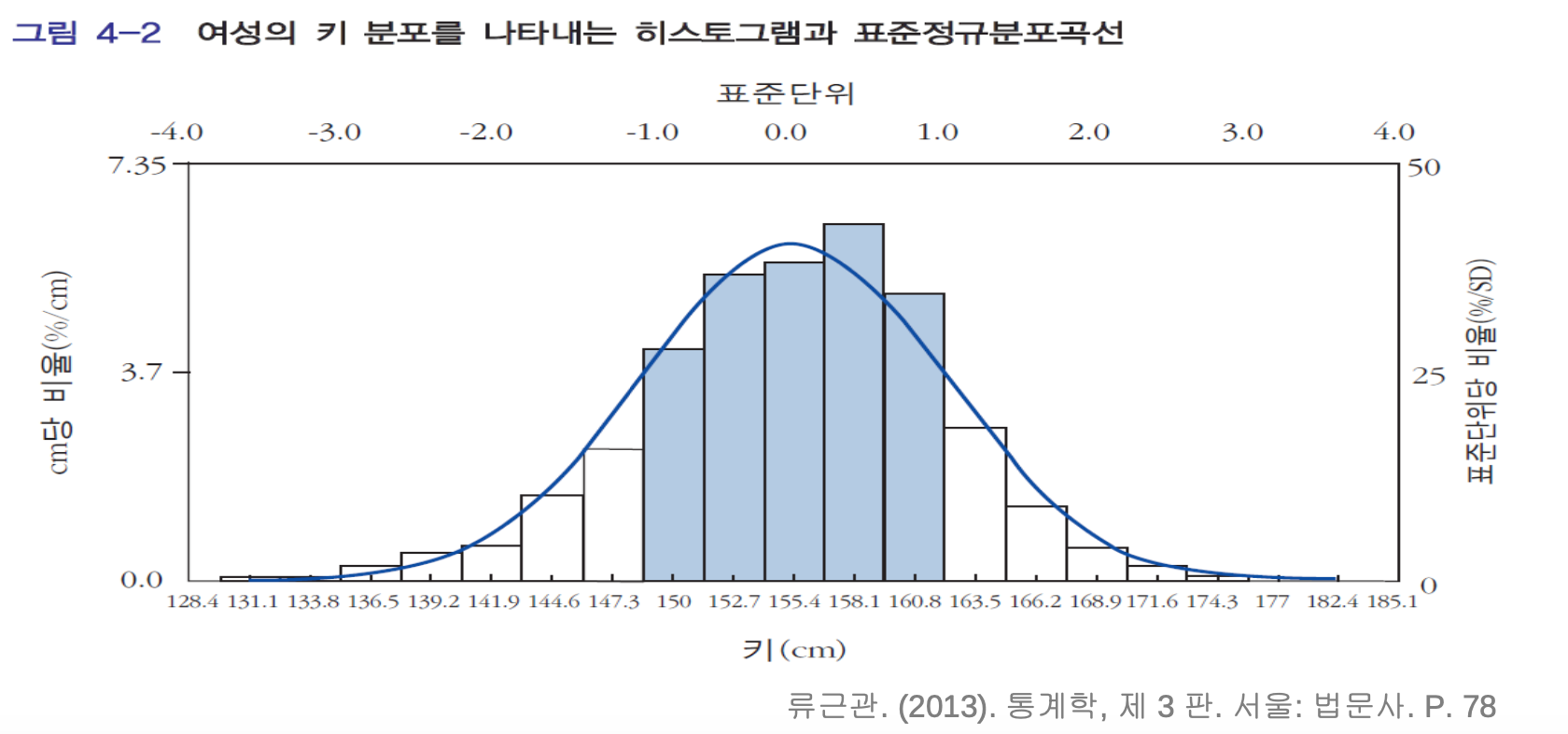
정규분포곡선의 모양

• 평균을 중심으로 좌우 대칭(symmetric)
• 종 모양(bell-shaped)
• 봉우리가 하나(single-peaked)

평균과 표준편차

• 정규분포곡선은 평균과 표준편차에 의해 그 모양이 완벽하게 묘사된다.
• 즉, 정규분포를 따르는 히스토그램은 중심과 중심 주위로 퍼진정도 등 두 정보만으로 100% 묘사된다.

분위수의 의미와 활용

백분위수의 정의

• 전체의 자료의 분포를100개의 구간으로 나누면 99개의 경계점 필요.
  • 전체자료의 분포를 면적이 같도록 둘로 나누기 위해서는 1개의 경계값이 필요했었다.(중앙값)
• 백분위수(percentile)는 하나의 히스토그램을 100개의 균등한 영역으로 나누는 99개의 경계점 값들.
• 제 p 백분위수는 그 값보다 작은 값이 p%, 큰값이 (100-p)%가 되는 경계값.
• 많은 히스토그램은 정규분포곡선과 다름.(평균과 표준편차만으로는 부족)
• 이러한 히스토그램을 요약할 때는 백분위수 개념이 유용.

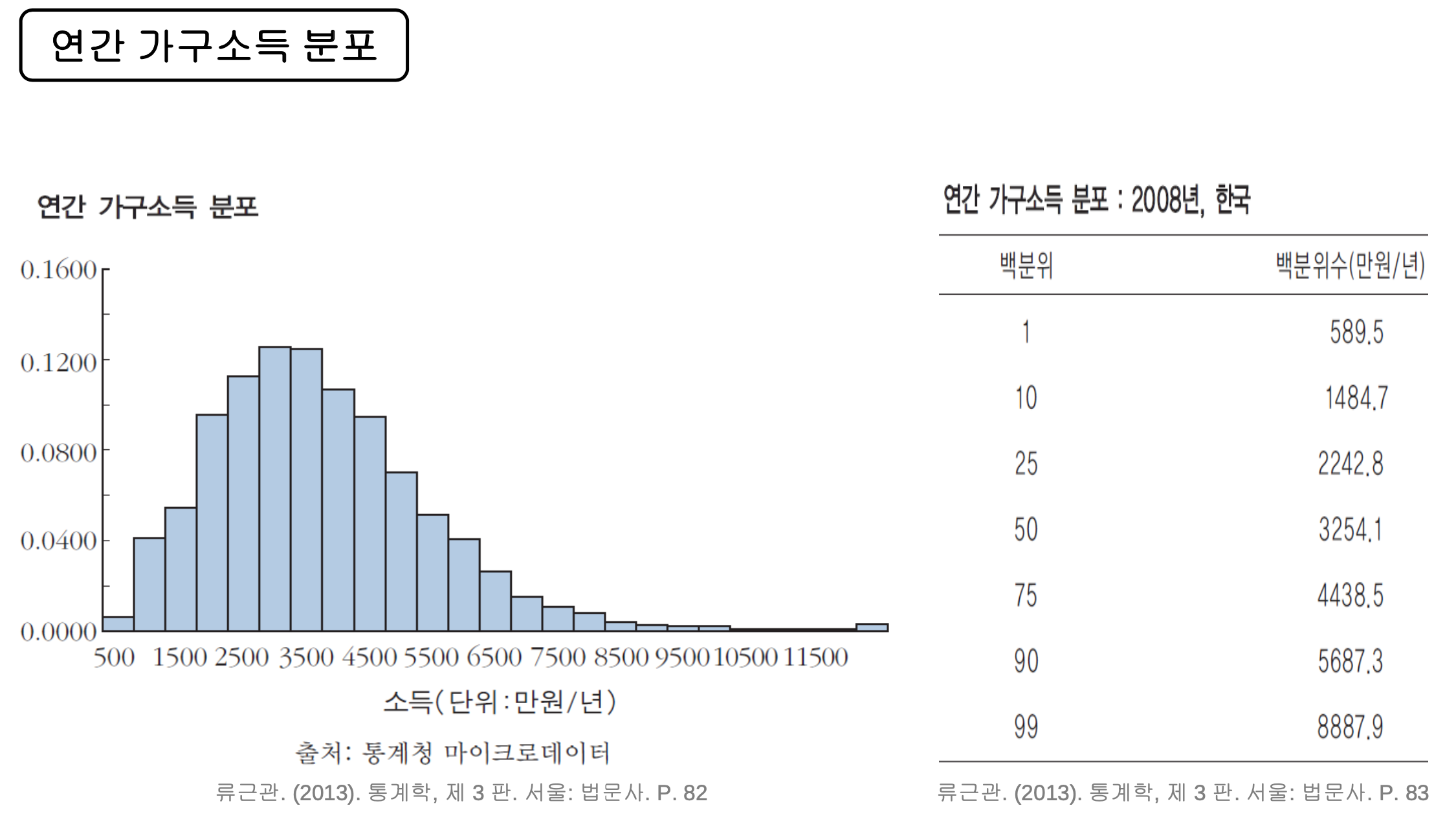
• 2008년 실제 데이터
• 좌우 대칭이 아님 (정규분포와 상당히 거리가 있음)
• 소득분포를 얘기할때는 percentile 정보를 많이 사용

사분위수

• 전체를 4개로 나눈 3개의 경계점.
• 상위 25%의 소득과 하위 25% 소득은 얼마정도 차이가 나는지 등을 비교해볼 수 있음.
• 백분위수 가운데 25번째, 50번째, 75번째 백분위수를 특별히 제1사분위수 (first quartile), 제2사분위수(second quartile), 제3사분위수(third quartile)라 부름.
• 50번째 백분위수는 제2사분위수이면서 중앙값(median)임.
• 사분위수 범위(interquartile range)
  • (사분위수 범위) = (제3사분위수) - (제1사분위수)
• 다섯 숫자 요약(five number summary): 최소값, 제1사분위수, 제2사분위수, 제3사분위수, 최대값
  • (최소값, 최대값) 쌍 대신 (제5백분위수, 제95 백분위수) 쌍 또는 (제1백분위수, 13 제99 백분위수) 쌍을 사용하기도 함

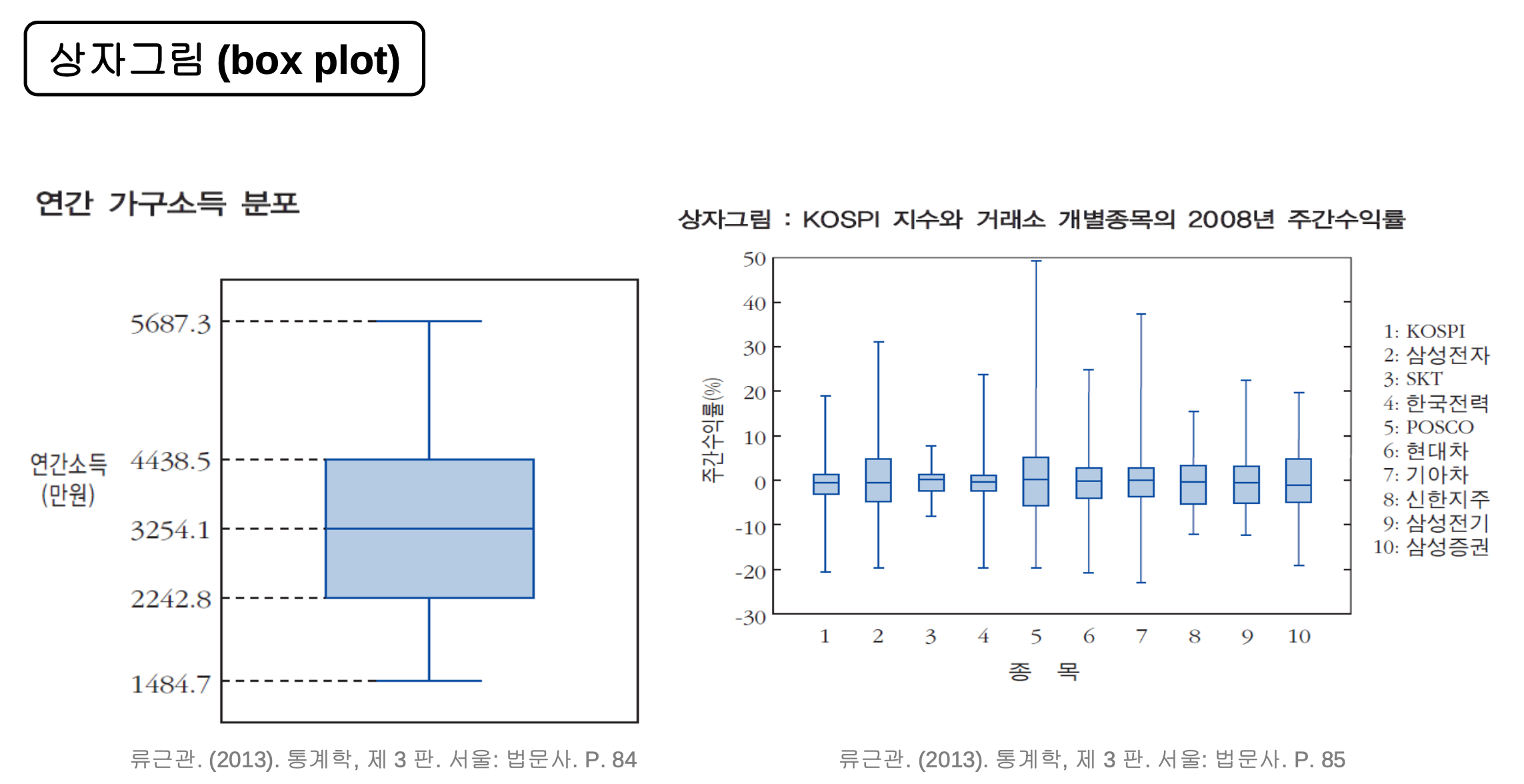
• 5개 숫자를 이용하여 상자그림으로 표현
• 서로 다른 자료를 비교하는데 도움이 될 수 있음

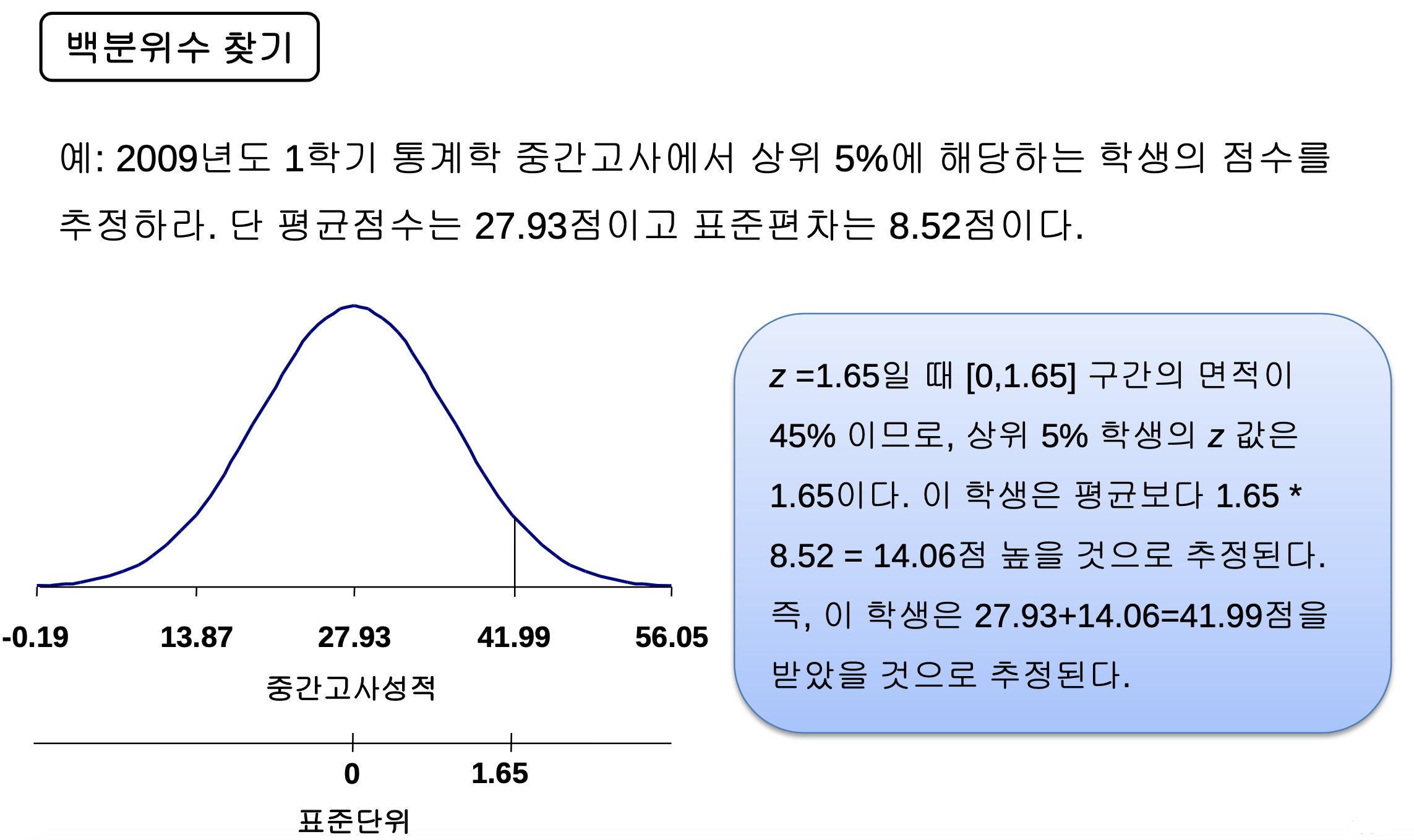
• 표준점수와 백분위수 사이의 관계

요약

• 자료의 특성을 수치화 하는 방법으로 평균과 표준편차가 있다.
• 표준편차는 평균으로부터 떨어진 거리를 나타낸다.
• (자료의 개수 - 1)을 표준편차 계산에 있어서의 자유도라고 한다.
• 숫자들의 약 68%가 평균으로부터 1SD 이내의 영역에 존재한다. 그리고 약 95%의 숫자들이 평균으로부터 2SD 이내의 영역에 존재한다. 이러한 68-95법칙은 경험적으로 많은 자료에서 성립한다.
• 개별 관측치에서는 측정오차가 포한되어 있을 수 있다. 동일한 상황하에서 측정을 반복한 뒤 그 관측치들의 표준편차로 개별 관측치에 포함된 측정오차의 표준적인 크기를 추정할 수 있다.
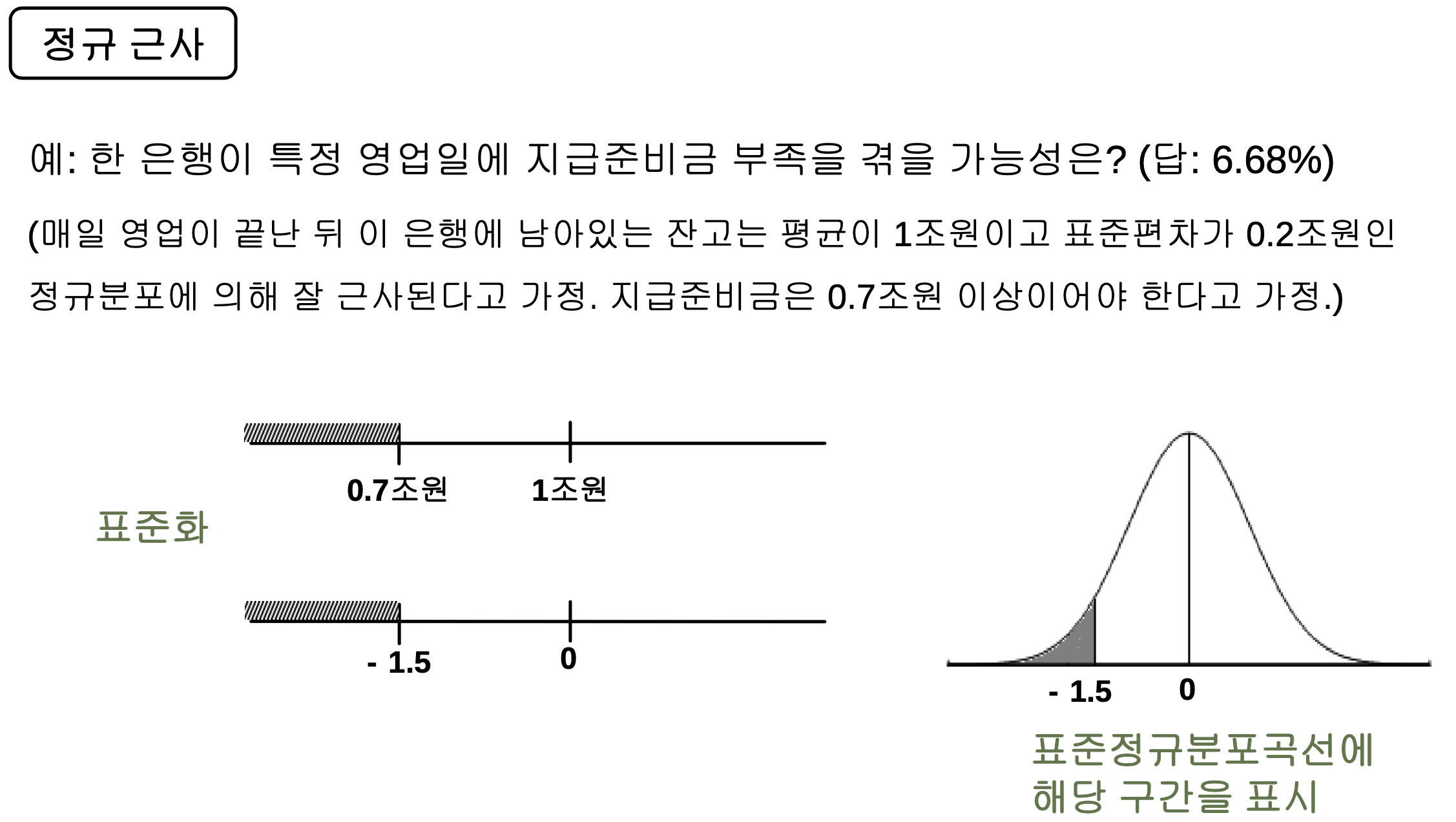
• 정규분포곡선은 평균을 중심으로 대칭이고, 종 모양을 띠고있으며, 봉우리가 하나이다. 정규분포곡선 아래 면적과 관련해서는 68-95-99.7 법칙이 성립한다.
• 숫자들이 정규분포곡선을 따른다면 자료가 어떤 구간 내에 어느 정도 비율로 분포되어 있는지 쉽게 알 수 있다. 구간을 표준단위로 바꾸고 표준정규분포곡선 아래 대응되는 영역의 넓이를 구하는 과정을 ‘정규분포의 근사’라고 부른다.