K-MOOC 경제통계학 1부 : 그림과 수치를 이용한 자료의 정리 강좌를 바탕으로 작성한 글입니다.

요약

• 통계학은 자료를 분석하는 학문이다.
• 통계학은 일부의 자료를 수집, 정리, 요약하고 이를 이용하여 전체의 특성에 대해 추론하는 작업을 포함한다.
• 자료를 정리하는 방법에는 그래프를 이용하는 방법과 수치를 이용하는 방법이 있다.
• 통계적 연구에는 실험적 연구와 경험적 연구가 있다.
• 경험적 연구의 경우 무작위로 통제된 실험에 대한 연구가 아니기 때문에 자료에 편의가 존재할 수 있다.
• 경험적 연구에서의 근본적인 문제는 처리집단과 통제집단 사이에 처리여부를 제외하고도 그 외의 많은 요인이 다르다는 점이고, 이에 따라 결과에 영향을 미칠 수 있는 기타의 요인을 통제할 필요가 있다.

심슨의 역설

• 실험자료가 아니라 경험적인 자료를 가지고 분석을 하다보면 잠복해있는 것을 통제 못해서 잠복해있는 요인의 영향을 공통으로 받는 X와 Y의 관계가 왜곡되서 나타날 수 있다. (중국의 경제성장 ; 공무원의 청렴도, 항만시설의 발전정도 등이 잠복해있어서 외국인의 투자유치에도 영향을 미친다.)
  -> 잠복해있는 혼동요인 때문
  -> 따로따로 분석하면 된다.

혼동요인 통제

나이를 통제 했을 때 피임약 복용하면 혈압이 조금 올라감

자연로그 변환의 역변환 : 지수

자료의 중심과 퍼진 정도

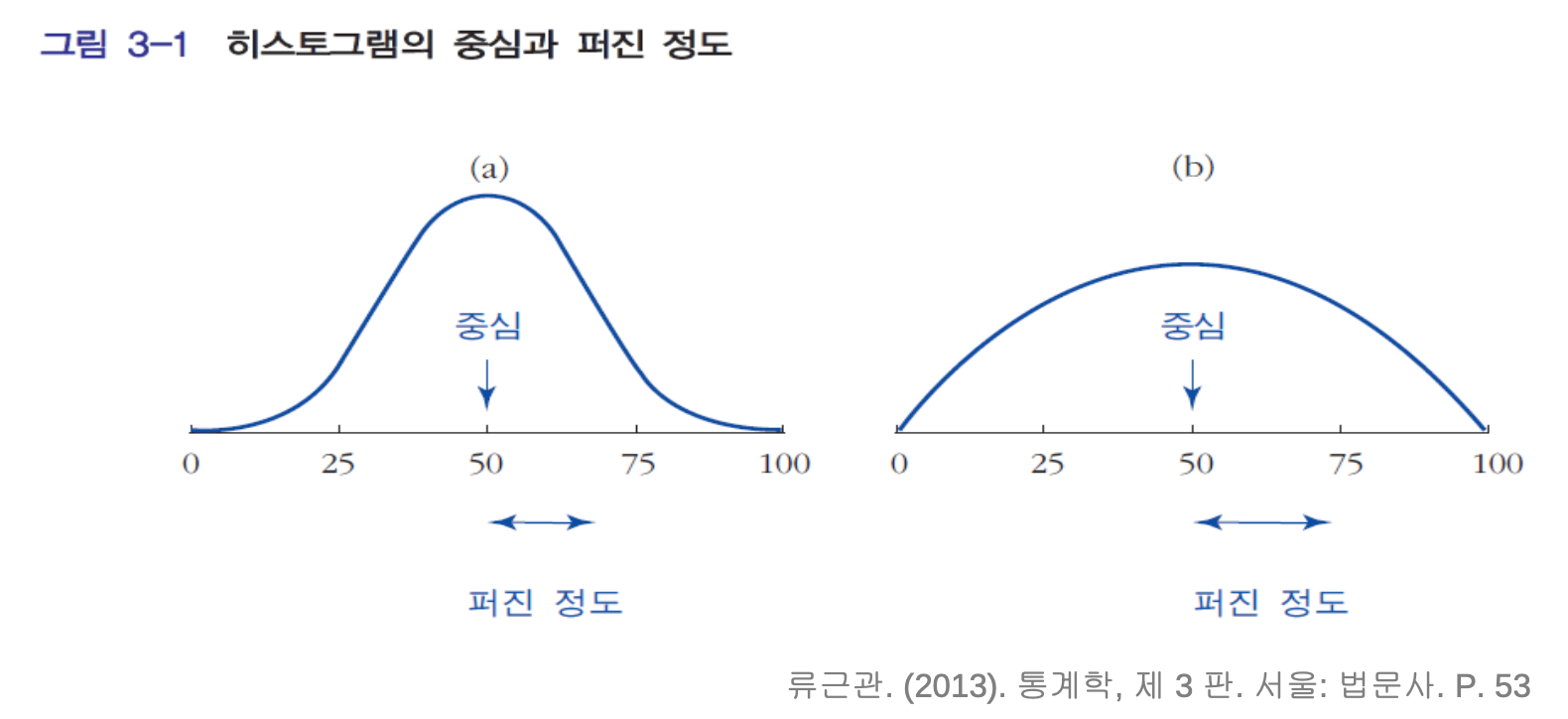
• 히스토그램에서 자료를 요약할 때 중심(평균, 중앙값)과 중심 주위로 퍼진 정 도(표준편차, 사분위수 범위)를 주로 사용
• 대표적으로 떨어져있는 거리가 첫번째 그림은 작고 두번째 그림은 크다. 중심은 같지만 편차는 두번째 그림에서 크다.
• 투자를 예로 들면 위험을 선호하는 타입이면 오른쪽 자산에 투자, 위험을 싫어하는 왼쪽 자산에 투자할 수 있다.

평균

• 평균(mean)은 관측치의 총합을 관측치의 개수로 나누어 구한다.
• 평균이 중요하지만 전부는 아님. 아래 세 그림은 평균이 같지만 퍼진 정도가 다름

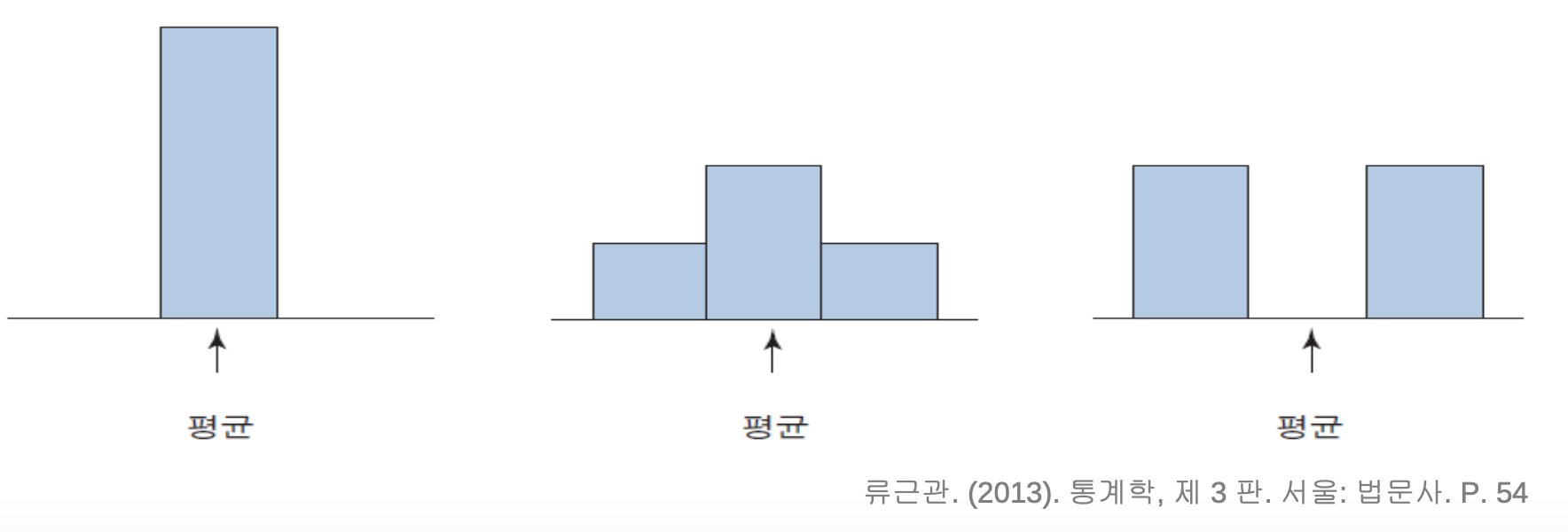
• 첫번째 그림의 경우 자료로 사용하는 모든 자료가 평균 근처로 모여있기때문에 평균만 알면 다아는 것.
  -> 평균에 담긴 의미가 굉장히 강함
  
• 두번째 그림의 경우 평균주위로 데이터가 모여있기때문에 평균만 알면 상당히 많은 것을 알수있는 상황.
• 세번째 그림은 평균은 평균인데 평균의 의미는 굉장히 취약하다. 평균근처에 데이터가 없음 -> 좌우 데이터를 균형시키지 못함.

중앙값(median)

• 절반이상의 숫자들이 이 값보다 크거나 같고 동시에 절반이상의 숫자들이 이 값보다 작거나 같은 수
• 히스토그램은 중앙값에서 그 면적이 양분됨
• 중앙값은 n 이 홀수이면 (n+1)/2번째로 크거나 작은 숫자임
• 중앙값은 n이 짝수이면 n/2번째 숫자와 (n+1)/2번째 숫자의 평균으로 정의
• median voter theorem: 중앙값이 LAD의 해로 얻어진다는 것과 수학적으로 같은 내용임. 선호의 비대칭분포 이용하여 후보자의 location choice 문제 설명.

최빈치(mode)

• 가장 빈번하게 발생되는 값
• 히스토그램은 최빈치에서 그 높이가 제일 높음

중앙값 정리 (Median Voter Theorem)

다수결에 의한 투표는 중앙값 투표자(median voter)가 선호하는 결과를 선택 하게 됨. 이는 중앙값이 LAD (least absolute deviation)의 해로 얻어진다는 것과 수학 적으로 같은 내용임

• 이는 유권자의 선호를 일차원 실직선상에서 표현할 수 있을때 성립함
• 유권자의 선호가 다차원적이면 성립하지 않음
• 정치 영역에서의 선거나 민간 영역에서의 비즈니스나 유사함
• 비즈니스맨이나 정치인 모두 공통적으로 “다수 투표자”의 표심을 얻고자 함
• 중앙값에 위치한 사람의 성향을 대표할 수 밖에 없다.

평균과 중앙값의 관계

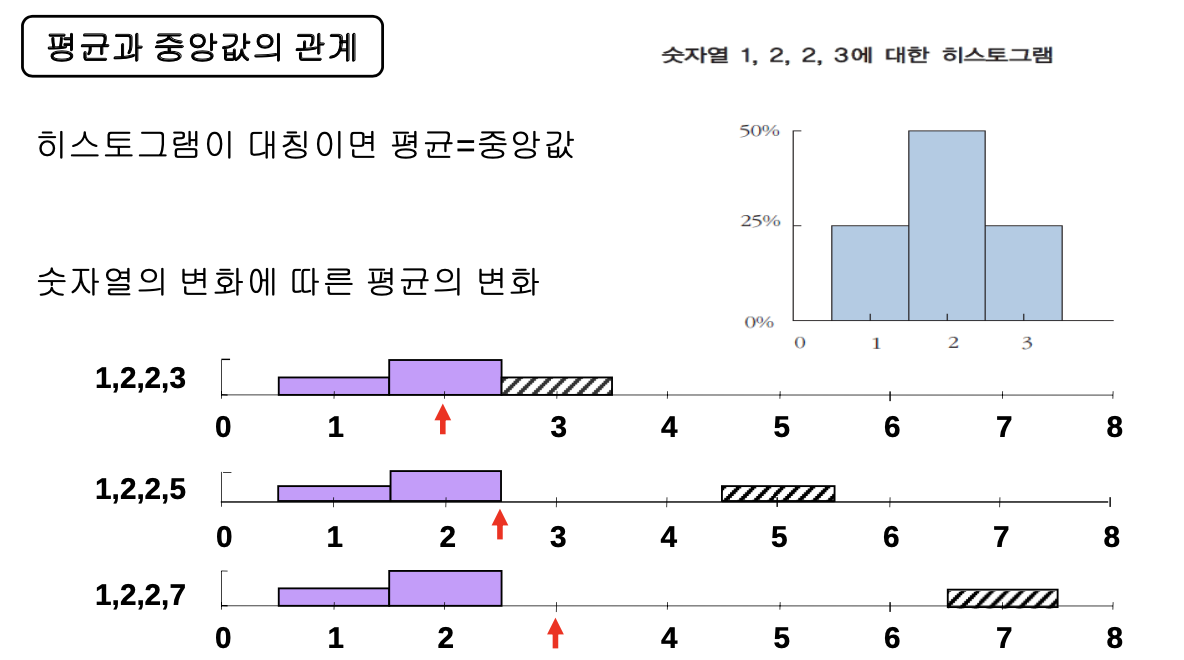
• 위의 세 히스토그램에서 중앙값은 언제나 2이나 평균은 화살표를 따라서 이 동
• 극단적인 값이 변화함에 따라 중앙값은 좀 더 강인한데 평균은 상당히 민감하게 반응

-> 1. 극단적인 값이 존재할 때 평균은 극단적인 값에 큰 영향을 받고 중앙값은 영향을 덜 받음

-> 2. 히스토그램이 좌우대핑이면 평균=중앙값

-> 3. 히스토그램 어느한쪽으로 치우치면(비대칭이면) 중심의 측도(measure)로 평균보다 중앙값이 더 적절할 수 있음.

히스토그램의 세 가지 꼬리 유형

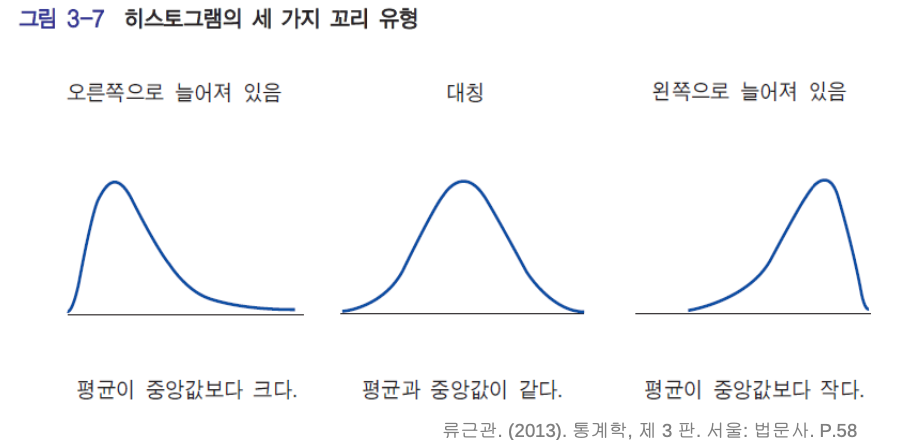
• 평균은 극단적인 값의 영향을 받음
• 중앙값은 극단적인 값의 영향을 받지 않음
• 극단적인 값이 존재하는 경우 평균보다 중앙값이 중심을 더 잘 나타냄
• 꼬리가 오른쪽으로 치우쳐져 있으면(=극단적인 값이 오른쪽에 치우쳐져 있으면) 중앙값은 덜 민감한데 평균은 오른쪽으로 따라가니까 오른쪽으로 끌려간 평균이 중앙값보다 오른쪽.
• 소득 분포는 오른쪽 그림과 같음(예를 들면 소수의 부자들이 세번째 그림임)

표준편차와 자유도의 직관적 의미

제곱근-평균-제곱(Root-Mean-Square)

계산은 표현의 역순(제곱 후 평균, 최종적으로 제곱근)

• (1) 제곱 (S) : 모든 수를 제곱하여 부호를 없앤다.
• (2) 평균 (M) : 제곱된 값들의 평균을 구한다.
• (3) 제곱근 (R) : 제곱-평균된 값에 제곱근을 취한다.

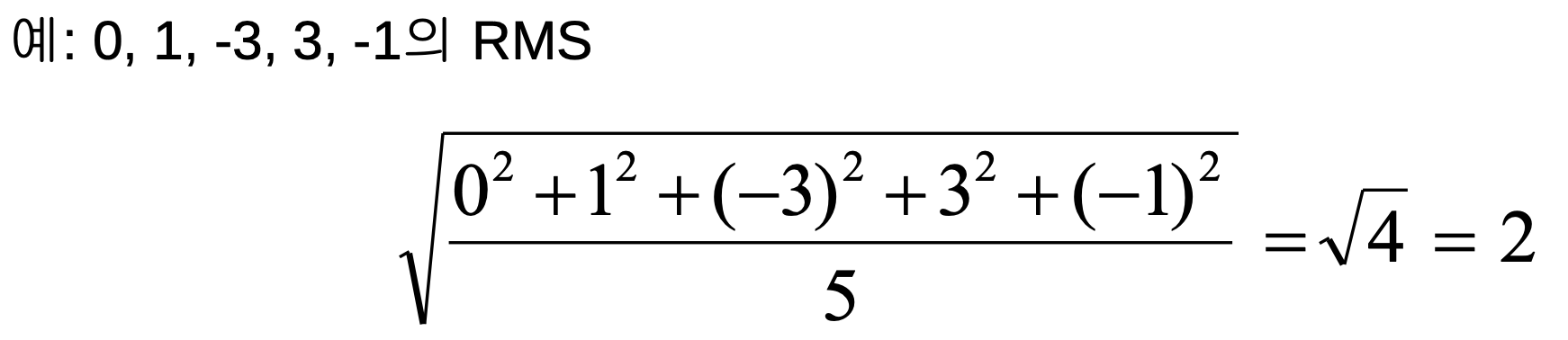
RMS란?

• 표준적인 편차를 재기위해서 그냥 합쳐서 평균하면 0이 되기때문에 캔슬링아웃을 막기위해 제곱을하여 평균을 구하고 최종적으로 제곱했던 효과를 중화시켜서 원래의 측정단위를 되돌려 받기 위해 제곱근을 취해주는 과정

표준편차란?

• 표준편차(SD)는 평균으로부터의 편차들의 RMS와 대략 비슷
• 표준편차는 관측치들이 평균으로부터 얼마나 떨어져 있는지 알려줌
• 다만 중간에 낀 M을 계산할때 10개의 편차를 더했으면 -1을해서 9개로 나눠야한다. (10개의 편차중에 자유로운 것은 9개 밖에 없다.)
• -1과 관련된 개념이 자유도(degrees of freedom; 주어진 조건 하에서 자유롭게 변화할 수 있는 개수)이다.
• 평균으로부터의 편차들을 다 더하면 0이된다.
• 10개의 편차가 있을 때 9개의 편차를 알면 10번째의 편차를 저절로 알 수 있다.

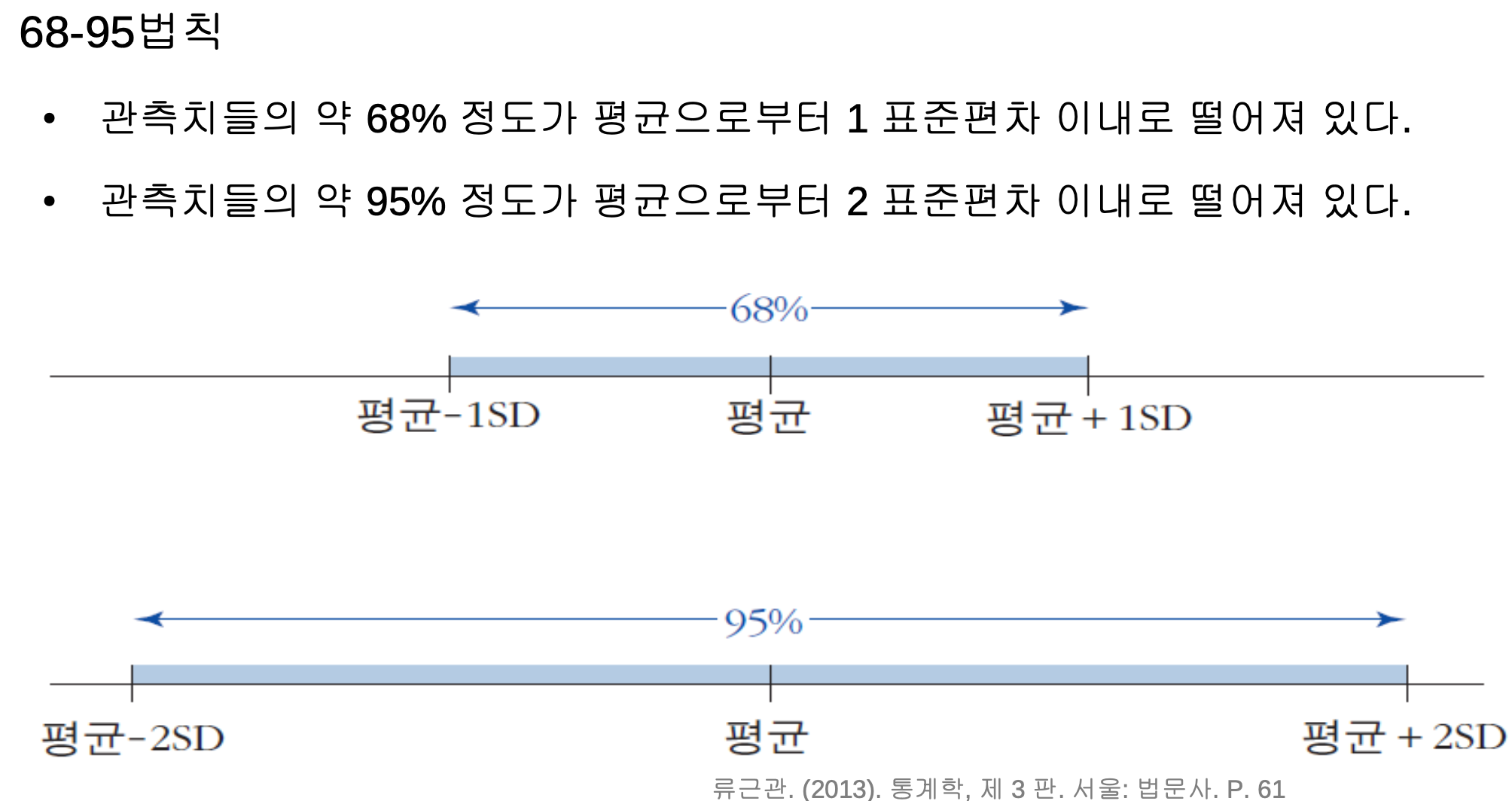
• 전체조건1 : 히스토그램의 모양이 봉우리가 하나
• 전제조건2 : 히스토그램이 좌우 대칭
• 전제조건3 : 양쪽으로 갈수록 감소하는 종모양

자유도(degrees of freedom)란?

• 자유도는 합쳐진 값들 중에서 실질적으로 독립인 값들의 개수
• 표준편차 계산하는 경우의 자유도는 자료의 개수 - 1
• 표준편차계산의대상이되는편차들의합은0이됨.편차들의합이0이된다 는 하나의 제약조건이 자유도를 1만큼 감소시킨 것임

예: 극단적으로 자료의 개수가 하나인 경우

• 편차는단하나뿐이고그값은0임
• 0에 대해 제곱의 평균, 즉 MS(mean square)를 구할 때 자유도 고려치 않으면 0/1=0이고 자유도를 고려하면 0/(1-1)=0/0으로 부정형(indefinite form)이 됨
• 단 하나의 자료만을 가지고는 퍼진정도를 알 수 없음. 이때 퍼진정도는 0이 아니라 ‘알 수 없다(부정형)’가 정답. 즉, 자유도를 고려해야 함

측정오차(measurement error)

• 관측치와 실제 값의 차이
• 측정오차가 존재하면, (관측치)=(실제 값)+(측정오차)
• 측정오차의 대략적인 크기는 관측치들의 표준편차(SD)를 통해 알 수 있음
• 표준편차(SD)의 크기는 한 번의 관측에서 측정오차가 어느 정도 될지 알려 줌

편의(bias)

• 방향성을 갖는 하나의 체계적인 오차
• 측정오차와 함께 편의가 있으면, (관측치)=(실제 값)+(편의)+(측정오차)

이탈값(outlier)

• 극단적인 관측치