K-MOOC 경제통계학 1부 : 그림과 수치를 이용한 자료의 정리 강좌를 바탕으로 작성한 글입니다.

산포도와 상관관계

결합분포

이제까지는 한 번에 하나의 변수만을 다루는 방법에 대해 살펴보았다.

• 이제부터는 두 변수 사이의 상호관계를 분석하기 위한 방법을 살펴본다.
• 남녀간의 관계처럼 많은 경우 둘간의 관계가 중요하다.
  • 예: 교육과 임금
  • 예: 통화증가율과 물가상승률
  • 예: 학급규모와 학생성적
• 결합분포(joint distribution): 두 변수간의 관계 전모를 보여줌

산포도 (scatter plot)

• 두 변수 사이의 관계를 살펴보기 위해 산포도를 이용한다.
• 설명변수는 x로 표기하고 가로축에 표시
• 피설명변수는 y로 표기하고 세로축에 표시

중간고사 기말고사 성적간 관계가 약한 경우

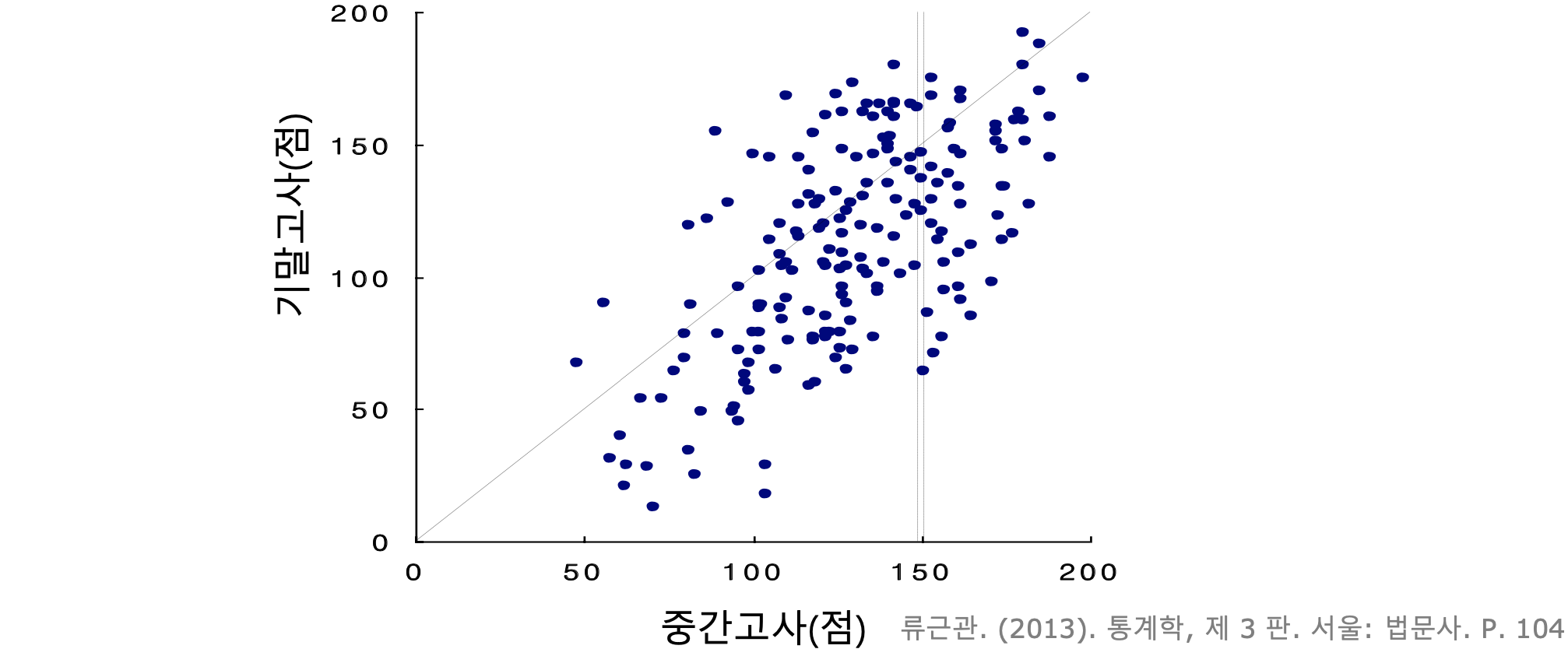
• 변수 사이의 관계가 약하면 한 변수 값이 다른 변수 값을 예측하는 데 큰 도움 안됨
• 중간고사에서 150점 받은 학생들의 기말고사 성적은 55점에서 175점 사 이에 분포

중간고사 기말고사 성적간 관계가 강한 경우

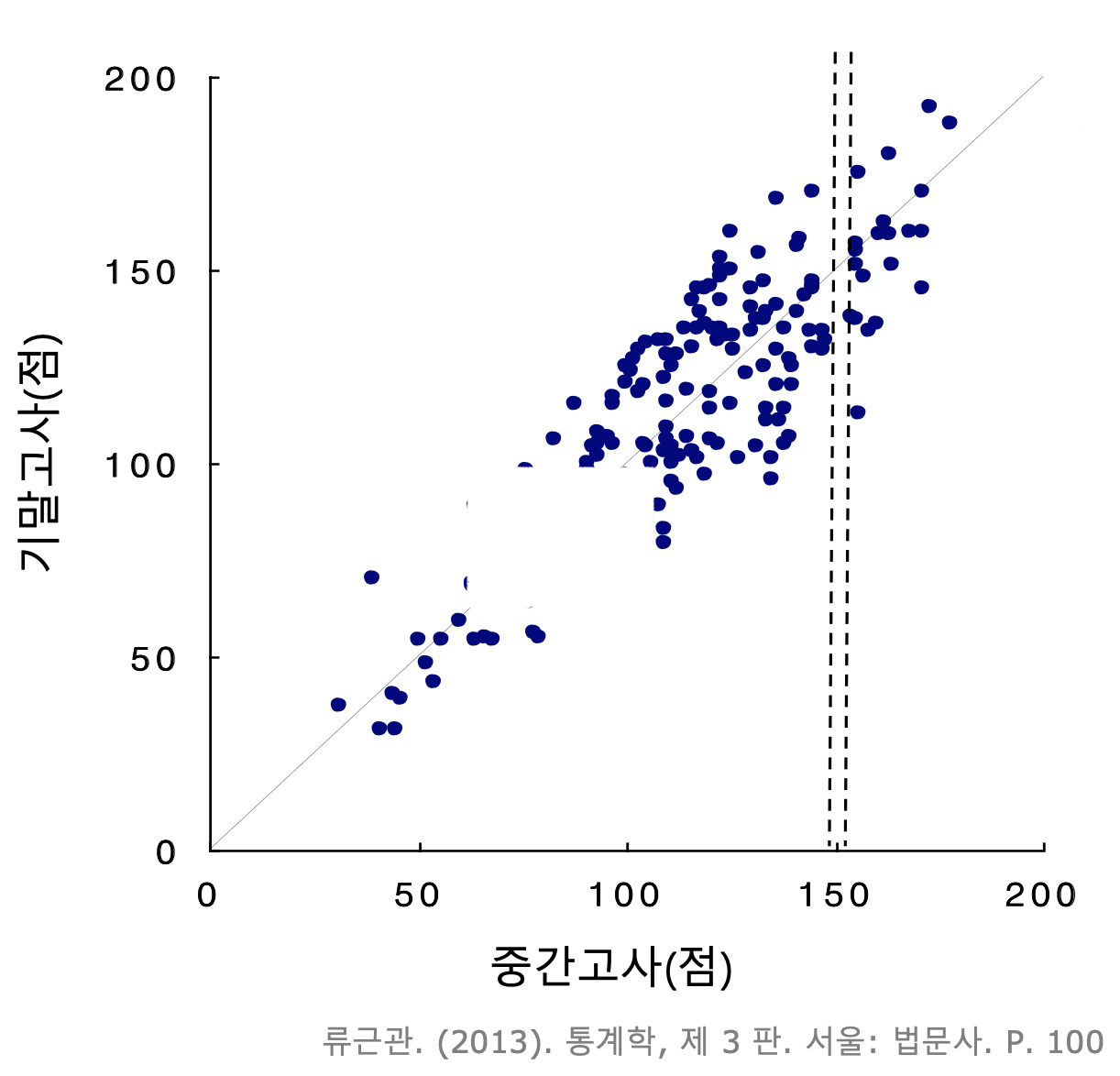
• 변수 사이의 관계가 강하면 한 변수 값이 다른 변수 값을 예측하는 데 크게 도움됨
• 중간고사에서 150점 받은 학생들의 기말고사 성적은 105점에서 175점 사이에 분포

산포도의 요약

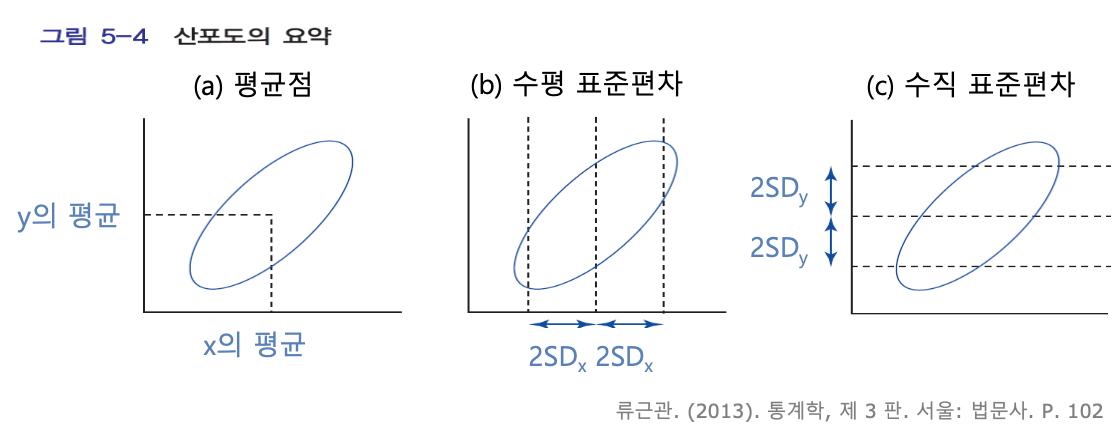
• 가로로 보면 대략 95%의 점들이 x평균점을 기준으로 2SDx 이내에 위치함
• 세로로 보면 대략 95%의 점들이 y평균점을 기준으로 2SDy 이내에 위치함
• x의 평균과 표준편차, y의 평균과 표준편차는 x와 y의 분포를 따로따로 요약

상관계수 구하기, 상관계수의 특징

상관계수의 필요성

:두 변수사이에 존재하는 방향과 강도를 측정

• 선형관계만 가능
• 한 변수가 증가하면 다른변수도 대체로 선형관계를 따라서 증가
• 강도는 상관관계가 절댓값이 0과 1사이에 위치하는데 1쪽으로 갈수록 선형관계가 강하고 0으로 갈수록 선형관계가 약하다.

가로든 세로든 평균과 표준편차가 동일해도 두 변수의 관계는 상이

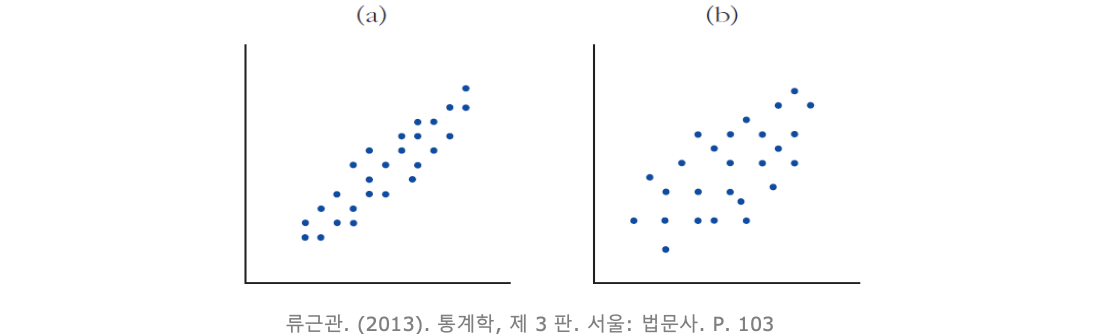
• 위의 두 산포도는 가로든 세로든 중심과 퍼진 정도가 동일하지만 (a)가 (b) 보다 더 강한 선형관계를 보임
• 두 변수간 선형관계의 방향과 강도가 얼마나 되는지 측정할 필요성 대두
• 상관계수는 두 변수간 선형관계의 방향과 강도 측정

두 변수 사이의 관계

이변량 자료의 요약 통계량

• x의 평균과 표준편차
• y의 평균과 표준편차
• x와 y간 상관계수 (correlation coefficient) : r로 표기

상관계수가 다른 여섯 개의 산포도

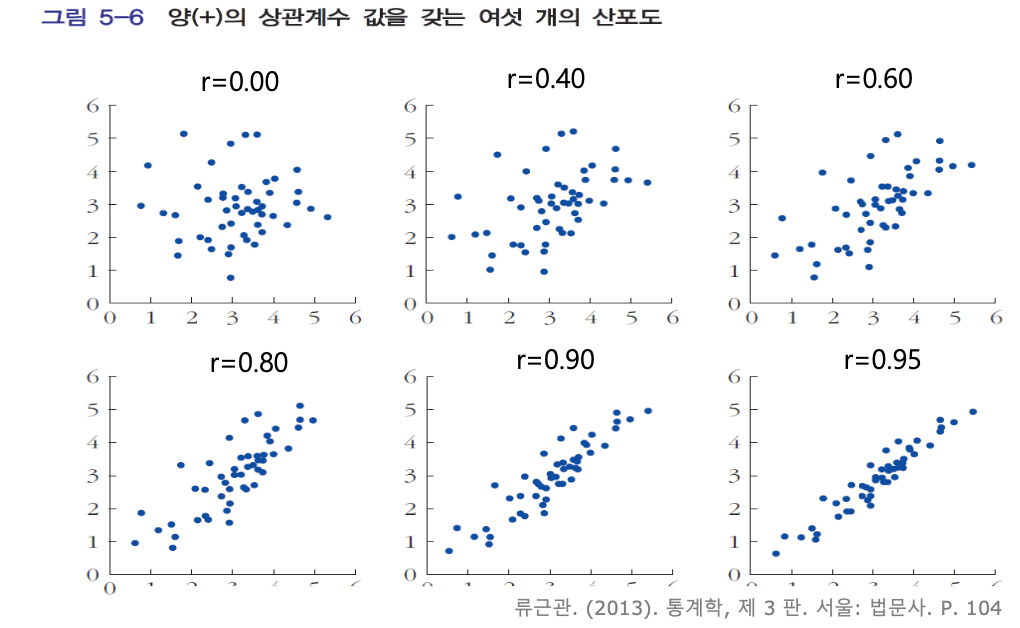
주: 각각의 산포도는 가로, 세로 모두 평균 3, 표준편차 1의 동일한 값을 갖는다. 각각의 산포도에는 50개씩의 점이 찍혀 있다.

• 두 점의 관계가 직선에 의해서 잘 묘사될수록 상관관계의 절댓값이 크다.

상관계수의 범위, 부호

범위 : -1 ≤ r ≤ 1

• 상관계수 = 1 또는 –1 이면 완전상관(perfect correlation)
• 모든 점들이 정확히 하나의 선 위에 위치
• 양의 상관관계이면 점의 분포가 우상향
• 음의 상관관계이면 점의 분포가 우하향
• 두 변수의 표준편차가 모두 0이면 상관계수를 정의할 수 없음
• 두 변수 중 어느 한 변수만의 표준편차가 0이면 상관계수는 0